투자에 있어서 위험과 불확실성이라는 두가지 개념에 대해 잘못 번역되었거나, 와전되어 유포되는 경우가 많습니다. 위의 링크는 그러한 위험과 불확실성의 차이점을 정확하게 설명하고 있습니다.
위험, 즉 risk라는 말은 미래에 발생 가능한 경우 또는 사건이 확정되지 않고 가변적인 경우를 말합니다. 그러나, 미래에 발생가능한 경우들을 모두 열거할 수 있으며, 그 발생가능성을 확률분포로 나타낼 수 있습니다. 이렇게 발생가능한 경우들을 열거하고, 그 가능성을 확률분포로 나타낼 수 있을정도가 되려면 과거에 엄청나게 많은 사례들이 데이터로 나와있어야 겠지요.
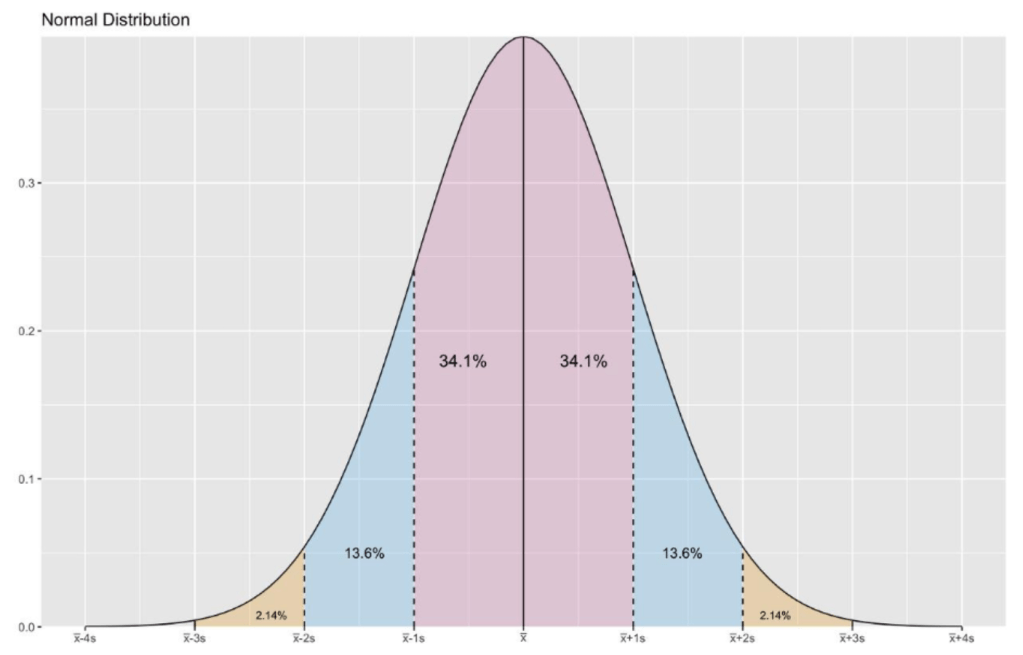
이를테면, 주가지수의 변동이 그렇습니다. 수십년 전부터 엄청난 데이터들이 컴퓨터로 분석되어있다 보니, 그 변동의 평균, 편차와 분산을 계산할 수 있습니다. 그래서 주가의 변동이 평균적인 표준편차보다 얼마나 벗어나서 움직였는지를 표현하는 데 2시그마, 3시그마 변동이라고 하는건 그러한 변동이 나올 확률이 통계적으로 13.6%(1-2시그마)나 2.1%(2-3시그마)였다고 말할 수 있는겁니다. 이렇게 확률분포 안에서 움직이고 표현가능한 변동성을 위험(risk)라고 할 수 있습니다.
최근 일어날 확률이 극단적으로 드문 사건들이 생각보다 자주 발생하는 현상을 이른바 “fat tail risk”라 부르는데, 이 또한 위험, 즉 risk의 범주에 포함되는 변동입니다. 다만, 정규확률분포보다 양 극단의 사건이 발생할 확률이 훨씬 더 높은 확률분포곡선을 따르는 것 뿐이지, 결국은 통계적인 범주 안에서 기술되고 이해될 수 있는 변동성이므로 위험의 범주에 포함되는거죠.
반면, 불확실성(uncertainty)은 발생가능성이 불확정되고 가변적인 건 같지만, 그 발생가능성을 객관적인 확률분포로 나타낼 수 없는 상태를 말하는 것입니다.
보통 투자영역에서는 경제학의 범주 안에서 계량화 해서 다룰 수 있는 사건들의 변동을 위험(risk)으로, 경제학의 범주를 벗어나서 계량화 할 수 없는 지정학적 리스크나, 정책에 의한 환경변화등을 불확실성으로 구분하고는 하는데, 이런 구분은 결국 “계량화” 할 수 있느냐 없느냐를 가지고 나누는 거지요.
하지만, 충분한 시계열을 두고 데이터를 모은다면, 불확실성도 충분히 통계처리가 가능한 위험의 영역에서 다룰 수 있는 변수가 될 수 있습니다. 설령, 불확실성을 계량화 하지 못하는 경우라도, 이게 문제될 건 없습니다. 왜냐하면 구태여 통계적인 계산이 아니라도 사람의 지혜와 상식, 그리고 통찰력이 있다면 그러한 불확실성을 감지하여 회피하거나 대처하는 게 불가능하지 않기 때문입니다. 계량화 할 수 없다고 해서 인간의 지혜와 상식으로 전혀 예상불가능하다는 건 아니니까요.
결국, 정말로 무서운 건 불확실성이 아니라, 잘못 계산되고 계량화 되는 위험측정입니다. 명백한 fat tail risk를 정규분포 확률곡선으로 설명하려 시도한다면, 그러한 시도는 반드시 막대한 손실과 투자실패를 필연적으로 초래할 것입니다. 대표적인 것이 각종 금융자산 가격의 변동성을 정규확률분포를 따르는 것으로 전제하고 투자계획을 짜는 경우입니다.
주가, 부동산, 채권 등등,,, 가끔씩 극단적인 상승이나 하락을 보이는 경우, 이를 3시그마 변동이니, 4시그마 변동이니 호들갑을 떨면서 자신의 투자실패를 “정말 정말 재수없게도 드문 일이 발생해서”라고 변명하는 경우들이 있습니다. 그런 엄청난 변동을 예상하지 못해 투자에 실패한 거라면, 이는 정말로 3시그마, 4시그마의 기적적인 일이 발생해서가 아니라, 평범하게 일어날 수 있는 변동이었음에도 fat tail risk를 대비하지 못했던 투자자들 자신의 안이함과 무능함 때문인겁니다.
각종 자산시장의 변동을 정규 확률분포대로 움직이는 것이라 잘못 상정하고 리스크의 위력을 과소평가하는 투자자는 단기적으로는 몇 번 성공할 지 몰라도, 장기적으로는 100% 돈을 모두 잃게 될 수 밖에 없다는 건 진리이자 필연입니다. 통계적으로 반드시 발생할 수밖에 없는 fat-tail risk를 발생하지 않는다고 잘못 전제하고 과감하게 리스크를 떠안는 투자를 하는데 망하는 건 수학적으로 필연일테니까요.
그런 의미에서 나심 탈레브의 책들은 투자자라면 꼭 읽어볼 필요가 있다고 봅니다.
